Page 121 - 《橡塑技术与装备》2025年2期

产品与设计
PRODUCT AND DESIGN

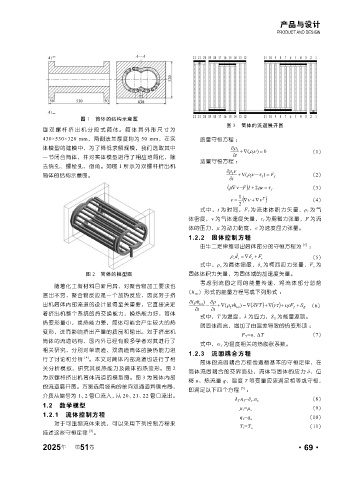
图 1 筒体的结构示意图
图 3 筒体的流道展开图
型双螺杆挤出机分段式筒体。筒体其外形尺寸为
430×530×320 mm，两侧法兰厚度均为 50 mm，在实 质量守恒方程 ：
体模型的建模中，为了降低求解规模，我们选取其中 ∂ρ ∂ρ ∂ρ
+
f f f
∂ρ ++ ( νρ ( νρ (∇ ρ ) = ) = ) ν 000= （1）
∇ ∇
f f f
∂t ∂t
f
一节闭合筒体，并对实体模型进行了相应地简化，除 ∂t + ∇ ( νρ f ) = 0
∂t
动量守恒方程 ：
去销孔、螺栓孔、倒角。如图 1 所示为双螺杆挤出机 ∂ νρ ∂ νρ ∂ νρ + ∇+ ∇+ -τ -τ -τν = = ) F FF=
∇( νρ ( νρ (ρ
f f f
∂ νρ
f
f
筒体的结构示意图。 t ∂ t ∂ t∂ + ∇( νρ f f f -τ f f f )) f ) = F f f f （2）
f
t ∂
ν νν
(µ (µ F )I + 2 e µ =+ 2 + µ = e2 e τττµ = f f f （3）
(µ∇ - )IF∇ - )IF∇ -
e τ
ν
(µ∇ - F f )I + 2 µ = 0 f
∂ρ
) =
∇
( νρ
)))
f
∇
T T T
e = e 111 + ∇ ∇ ∇+ ν νν （4）
( ν +∇ ( ν +∇ ( ν
e = 1 = ∂t
2 ( ν +∇ 2
e = 2 ∇ ν T )
2
式 中，t 为时间，F s s s F FF+ s s s
d = ∇= δ ∇= δ f 为流体体积力矢量，ρ f 为气
 
ρ dd
∇δ
   ρ∂
s   s ss νρ
ρ
+ +
)
+ (ρ
F
d =
=
ρ
f
F -τν
s s
∇δ∇+
f
s f
s
s
f
s
t ∂
体密度，v 为气体速度矢量，τ f 为剪载力张量，F 为流
∂ρ
∂( ∂( ∂(
h ρ h ρ h ρ
)) )
0
f
∂ρ ∂ρ ∂ρ (∇+
ν
ρ
体的压力，μ ) −− + + ∇ ρ ( ∇ ρ ( ∇+ ( ) = h ν h ν h ν )) ) ∇ λ λλ T TT ( )+υρντ ( )+υρντ ( )+∇ υρ SSS
tot tot tot为动力黏度，e 为速度应力张量。
) ∇+ ) ∇+ )+ ντ
F + ++
= ∇==
ρ
( ∇ ( ∇ ( ∇∇
FF
h ρ
∂(
− ∂ρ
f
tot ∂t
tot tot tot µ =+ 2
e τ
ν
f f f )IF
(µ∇ -
EE E
f f f
t ∂ + (
t ∂ t ∂ t ∂
− ∂ t ∂
h ν
∇ ρ
t
( ∇ f
f
f
t ∂
t ∂
1.2.2 固体控制方程 tot ) = ∇ λ T ) ∇+ ( )+υρντ F + S E
1
∂ νρ e = T T ∇ ⋅ ∇ ∇⋅ ⋅ T TT∇ ∇ ν T ) [6]
f =α =α =α
T f f
T T T ( ν +
T F
∇(ρ
f
⋅
∇ =
+
f =α )-τν
由牛二定律推导出筒体部分的守恒方程为 ：
T 2
f
T f
f
t ∂
 
ρ s d = ∇δ s + F s （5）
s
ν
µ =
)I + 2
e τ
F
(µ∇ -
式中，ρ s 为筒体密度，δ s 为柯西应力张量，F s 为
f
∂( h ρ tot 1 ) ∂ρ
f )
)
−
h ν
) ∇+
( ∇
+
( )+υρντ
=
T
∇ λ
∇
图 2 筒体的模型图 固体体积力矢量，为固体域的加速度矢量。 F + S E
e =
ν
∇ ρ ( T
( ν +∇
tot
f
t ∂ 2 t ∂
考 虑到 流 固 之间 的 能量 传 递， 将流 体 部 分总 焓
随着化工新材料日新月异，对聚合物加工要求也 ρ s d = ∇δ s + f =α T ⋅ ∇ T
 
F
T s
s
（h tot ）形式的能量方程写成下列形式 ：
层出不穷，聚合物反应是一个放热反应，因此对于挤
∂( h ρ ) ∂ρ
( ∇
出机筒体内部流道的设计显得至关重要，它直接决定 tot − + ∇ ρ ( h ν ) = ∇ λ T ) ∇+ ( )+υρντ F + S E （6）
t ∂ t ∂ f tot f
着挤出机整个系统的热交换能力，换热能力好，筒体
式中，T 为温度，λ 为应力，S E 为能量源项。
f =α
⋅
∇
T
热变形量小，换热能力差，筒体可能会产生较大的热 T T
就固体而言，增加了由温差导致的热变形项 ：
变形，进而影响挤出产量的质品和输出。对于挤出机
F T =α. ΔT （7）
筒体的流道结构，国内外已经有很多学者对其进行了
式中，α T 为温度相关的热膨胀系数。
相关研究，分别对单流道、双流道筒体的换热能力进
1.2.3 流固耦合方程
行了讨论和分析 [4] 。本文对筒体内部流道也进行了相
筒体的流固耦合方程也遵循基本的守恒定律，在
关分析模拟，研究其换热能力及筒体的热变形。图 2
筒体流固耦合的交界面处，流体与固体的应力 δ、位
为双螺杆挤出机筒体流道的模型图。图 3 为筒体内部
移 u、热流量 q、温度 T 等变量应该满足相等或守恒，
的流道展开图。方案选用经典的单向双通道异侧布局， [5]
即满足以下四个方程 ：
介质从编号为 1、 2 管口流入，从 20、 21、 22 管口流出。 .
δ f n f =δ s .n s （8）
1.2 数学模型 μ f =μ s （9）
1.2.1 流体控制方程 q f =q s （10）
对于可压缩流体来说，可以采用下列控制方程来 T f =T s （11）
描述这些守恒定律 [5] 。
2025 第 51 卷 ·69·
年